Math 215 Examples

Key Concepts

Vector-Valued Functions

A vector-valued function is a function that outputs a vector rather than a single number. Often we will be working with functions whose outputs are vectors in three-dimensional space. Such a function can be written as \[ \vec r(t) = \langle x(t), y(t), z(t) \rangle \] where \(f(t)\), \(g(t)\), and \(h(t)\) are usual functions whose outputs are single numbers (sometimes called scalar functions in contrast with vector-valued functions).

Space Curves

A vector-valued function \(\vec r(t)\) whose values are three-dimensional functions traces out a space curve, a curve in three-dimensional space.

For example, \[ \vec r(t) = \left\langle t, \frac{t^3}{18},\frac{t^2}{3} \right\rangle \] traces out a space curve called a twisted cubic:

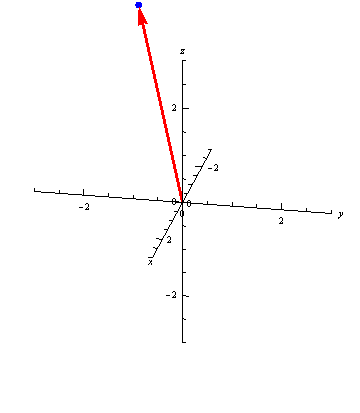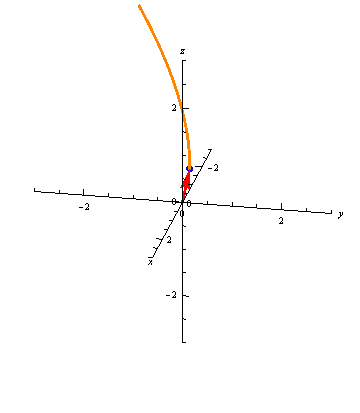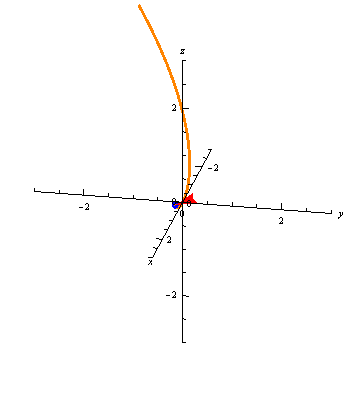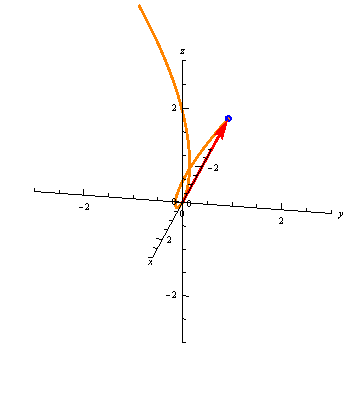
Vector-valued functions don't always trace out smooth curves. For example, \[ \vec r(t) = \left\langle \frac{t^4}{30}, \frac{t^3}{10}, \frac{t^2}{5} \right\rangle \] has a sharp corner at the point \(\vec r(0) = \langle 0, 0, 0\rangle\):

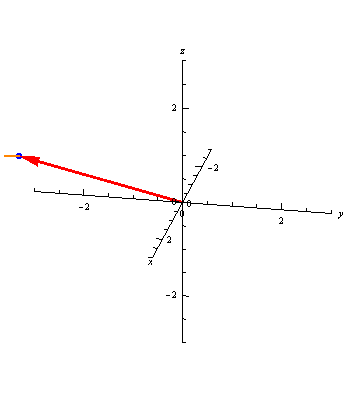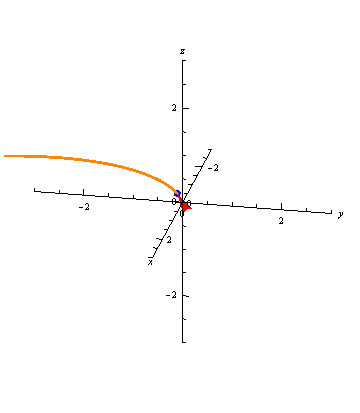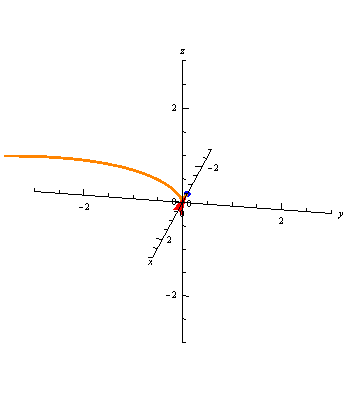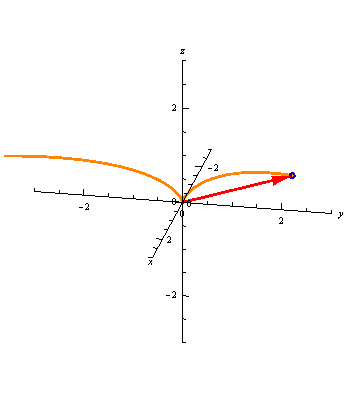
Different Parameterizations

Note that two different vector-valued functions may trace out the same curve. We say that two such vector-valued functions corresponding to the same curves are different parameterizations of the same curve.

Given any vector-valued function \(\vec r(t)\), it is easy to construct different parameterizations of the same curve: just use \(\vec s(t) = \vec r(at)\) for any non-zero constant \(a\).

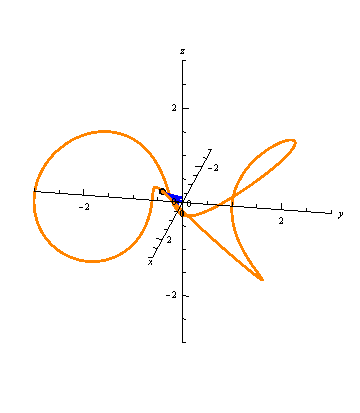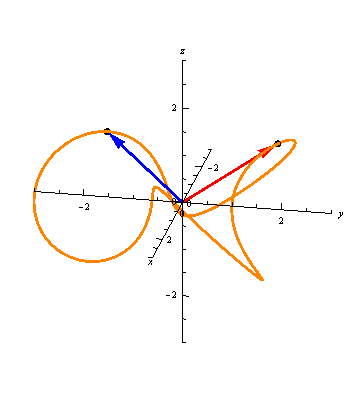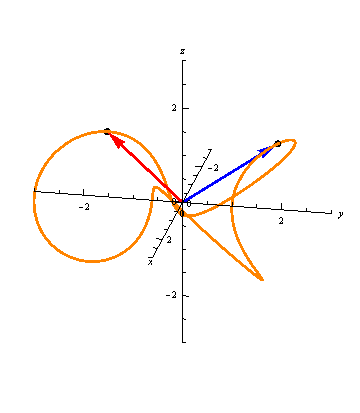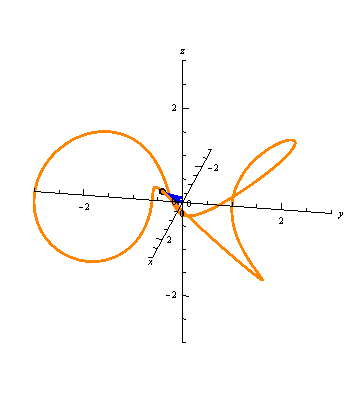
For example, suppose we have \[\begin{aligned} \vec r(t) &= \langle (2+\sin{3t})\cos{t}, (2+\sin{3t})\sin{t}, \cos{3t} \rangle \\ \vec s(t) &= \langle (2+\sin{6t})\cos{2t},(2+\sin{6t})\sin{2t}, \cos{6t} \rangle. \end{aligned}\] Notice that \(\vec s(t) = \vec r(2t)\), so as observed above, both these vector-valued functions will trace out the same space curve (a curve called a toroidal spiral):

Illustrated Example

Worked Solution

Since every equation in this problem is a function of \(x\), we can use \(x\) itself as our parameter. In other words, in our eventual parameterization \[ \vec r(t) = \langle x(t), y(t), z(t) \rangle, \] we can set \(x(t) = t\).

Since our curve lies entirely in the plane \(y=x\), it follows that \(y(t) = x(t)\) in our parameterization, or \(y(t) = t\). Since the curve lies on the paraboloid \(z = x^2 + y^2\), we similarly have \[ z(t) = x(t)^2 + y(t)^2 = 2t^2. \]

Thus our final parameterization of this curve is \[ \vec r(t) = \langle t, t, 2t^2 \rangle. \]

Visualizing the Example

The animation below shows the paraboloid \(z=x^2+y^2\) with \(\vec r(t) = \langle t, t, 2t^2\) tracing out its intersection with the plane \(y=x\):

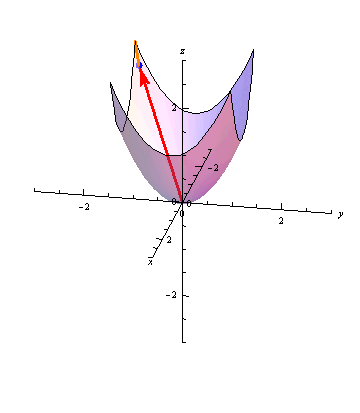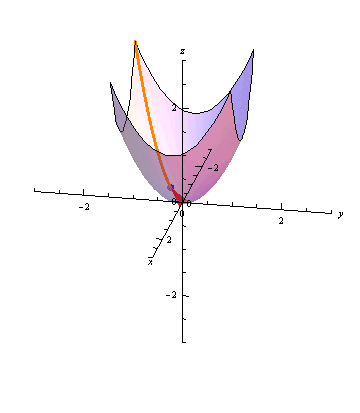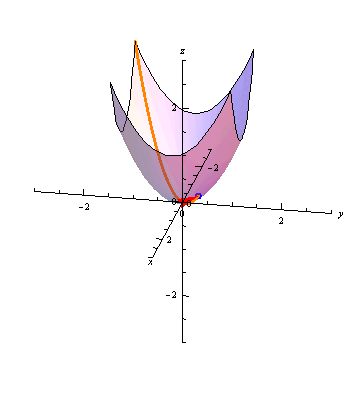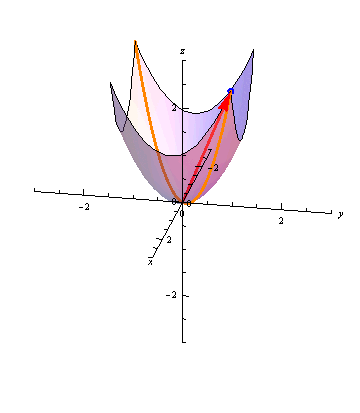
Further Questions

1. Find a parameterization of the curve in the example that traces out the curve half as fast.
2. Find a parameterization of the curve in the example that traces out the curve backwards.
3. What curve does \(\vec r(t) = \langle t, -t, 2t^2 \rangle\) trace out?
4. In the animation in Key Concepts with two different parameterizations, which of \(\vec r(t)\) and \(\vec s(t)\) is represented by the blue arrows? Which is represented by the red arrows?

Using the Mathematica Demo

All graphics on this page were generated by the Mathematica notebook 13_1SpaceCurves.nb.

This notebook generates images and animations like those on this page for any curve.

As an exercise, use the notebook to provide a visual demonstration illustrating your answers to Questions 1-3.

Investigate other vector-valued funtions \(\vec r(t)\). Can you find one that traces out a circle? A helix? Can you find one with a sharp corner somewhere other than the origin? Experiment with functions that yield sharp corners; can you figure out what causes them?