Key Concepts
Center of Mass
Let \(L\) be a lamina with density function \(\rho(x,y)\). Then the mass of \(L\) is \[m = \iint\limits_L \rho(x,y)\,dA.\] We also define its moment about the \(x\)-axis as \[M_x=\iint\limits_L y\,\rho(x,y)\,dA\] and its moment about the \(y\)-axis as \[M_y=\iint\limits_L x\,\rho(x,y)\,dA.\] Be careful: It's \(y\) that appears in the double integral defining \(M_x\), and \(x\) that appears in the double integral defining \(M_y\).
Moments are closely related to the intuitive notion of center of mass:
Once again, be careful: The \(x\)-coordinate of the center of mass is calculated by using \(M_y\), the moment about the \(y\)-axis, and the \(y\)-coordinate is calculated with \(M_x\). Keep in mind when working with moments that the notation may be counter-intuitive, as \(M_x\) corresponds to \(\bar y\) and has the extra \(y\) in the double integral. However, when working directly with center of mass, the two points of confusion cancel each other out, as if we expand out the definition of center of mass, \[\bar x = \frac{1}{m}\iint\limits_D x\,\rho(x,y)\, dA\] and \[\bar y = \frac{1}{m}\iint\limits_D y\,\rho(x,y)\, dA,\] with the extra \(x\) in the double integral for \(\bar x\) and the extra \(y\) in the double integral for \(\bar y\).
Visualizing Center of Mass
Imagine that we are trying to balance our lamina on a thin wall given by the line \(y=y_0\) for some constant \(y_0\). Then the lamina will balance if and only if \(y_0=\bar y\):

If our wall is even slightly off, then the lamina will fall:

The further from \(\bar y\) we are, the faster it falls:

Similarly, if our wall has the equation \(x=x_0\) for some constant \(x_0\), then it will balance if and only if \(x_0=\bar x\):

Again, for other values of \(x_0\), the lamina will fall:

If now we want to balance on a single point \((x_0,y_0)\), what point should we pick? If \(x_0\ne \bar x\), then as we just saw, the lamina will tilt and fall in the \(x\)-direction, and if \(y_0\ne \bar y\), it will similarly tilt and fall in the \(y\)-direction. To balance perfectly, then, we must balance on the center of mass \(\bar x,\bar y\):

Otherwise, as expected, the lamina falls:

Illustrated Example
Worked Solution
The lamina \(L\) is the type I region bounded above by \(y=\sqrt{1-x^2}\) and below by \(y=0\), for \(-1\le x\le 1\). Therefore, we will be able to write double integrals over \(L\) as iterated integrals with these bounds.
First we must compute the mass. Since the density is \(\rho(x,y)=1\), the integrand is just \(1\). The mass is therefore \[m = \iint\limits_L dA.\] While we could use techniques of integration to evaluate this, we can also recognize this as simply computing the area of \(L\). Since the area of the unit circle is \(\pi\), the area of \(L\), the unit semicircle, is just \(\frac{\pi}{2}\).
We next find \(\bar x\) first. Since our density function is \(\rho(x,y)=1\), our integrand is \(x\,\rho(x,y) = x\). We compute \[\begin{aligned} \bar x &= \frac{1}{m}\iint\limits_L x\,dA \\ &= \frac{1}{m}\int_{-1}^1\int_0^{\sqrt{1-x^2}} x\,dy\,dx \\ &= \frac{1}{m}\int_{-1}^1 xy\Big|_0^{\sqrt{1-x^2}}\, dx \\ &= \frac{1}{m}\int_{-1}^1 x\sqrt{1-x^2}\, dx \\ &= -\frac{1}{3m}(1-x^2)^{3/2}\Big|_{-1}^1 \\ &= -\frac{1}{3m}((1-1) - (1-1)) = 0. \end{aligned}\]
To find \(\bar y\), again since our density function is \(\rho(x,y)=1\), our integrand is just \(y\). We compute \[\begin{aligned} \bar y &= \frac{1}{m}\iint\limits_L y\,dA \\ &= \frac{1}{m}\int_{-1}^1\int_0^{\sqrt{1-x^2}} y\,dy\,dx \\ &= \frac{1}{m}\int_{-1}^1 \frac{1}{2}y^2\Big|_0^{\sqrt{1-x^2}}\, dx \\ &= \frac{1}{m}\int_{-1}^1 \frac{1}{2}(1-x^2)\, dx \\ &= \frac{1}{2m}\left(x-\frac{x^3}{3}\right)\Bigg|_{-1}^1 \\ &= \frac{1}{2m}((1-1/3)-(-1+1/3)) = \frac{2}{3m}. \end{aligned}\] Since we previously computed \(m=\frac{\pi}{2}\}\), we can plug this in, yielding \(\bar y = \frac{4}{3\pi}\).
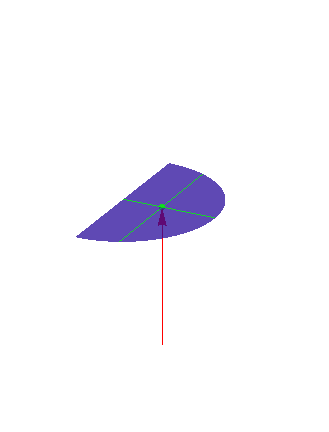
The center of mass is therefore \((0,\frac{4}{3\pi})\).
Visualizing the Example
The fact that \(\bar x=0\) should agree with our intuition, as the semicircle is symmetric about the \(y\)-axis:
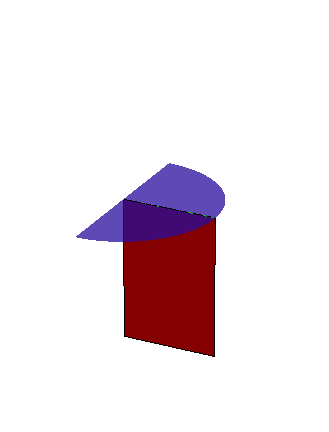
Do keep in mind, however, that if the density of the semicircle were not constant, then it may not balance on the line \(x=0\). In the following animation, the density function \(\rho(x,y)=x+1\) is used, and darker colors indicate greater density:

The \(y\)-coordinate of the center of mass is almost impossible to determine intuitively ahead of time. Still, we can say at least a little bit without doing any calculation. Since the semicircle is wider at the bottom than at the top, we can see that \(\bar y < \frac{1}{2}\). We can see that the semicircle does fall if we try to balance on \(y=1/2\):

The semicircle does not fall very quickly, however, suggesting that we must be close to the right \(y\)-coordinate. The actual value of \(\bar y\) is, as we computed, \(\frac{4}{3\pi}\approx 0.42\), which is indeed quite close to \(y=1/2\).
Putting both the coordinates together gives us the precise point \(\left(0,\frac{4}{3\pi}\right)\) on which to balance the semicircle:
Further Questions
- We observed that symmetry would have allowed us to conclude \(\bar x=0\) from the start. At what point in the actual calculation does it become clear?
- We saw that using the density function \(\rho(x,y)=1+x\) breaks the symmetry and results in a nonzero \(\bar x\). How would \(\bar y\) change with this density function? Try to answer this question without doing any calculation, then do the calculation to verify your answer.
- Is it always true that the center of mass of a lamina lies in the lamina itself? Justify your answer or give a counterexample.
Using the Mathematica Demo
All graphics on this page were generated by the Mathematica notebook 15_5MomentsAndCenterOfMass.nb.
This notebook generates animations like those on this page. You can specify any density function, any region, and any support point, and it will generate an animation of the lamina's motion.
As an exercise, use the notebook to provide clear graphical answer to Question 2 above.
Note that the shape of the lamina is entirely determined by regionFunction, so coming up with an interesting shape for a lamina involves finding an interesting regionFunction. Try searching (in a textbook or online) for interesting graphs of implicit functions and using their formulas as the regionFunction!